1.前言
点支承玻璃幕墙技术是从国外发展起来的,早在上世纪六七十年代国外就开始了点支承玻璃幕墙的应用,其中比较著名的工程有:法国建筑师安德良在纪念法国大革命200周年的十大建筑物之——拉维莱特科学馆的立面中所设计的点支承玻璃幕墙i著名的华裔建筑大师贝聿铭在法国卢浮宫改建工程地下广场的中心部位设计的金字塔形点支玻璃采光顶。我国的点支承玻璃幕墙技术上世纪九十年代由国外引进,其中最具标志性的建筑是1996年由法国夏邦杰建筑师事务所设计的上海大剧院工程。该I程的成功应用引起了国内建筑与幕墙行业的高度关注,点支承玻璃幕墙在中国高速发展起来。经过十多年的发展,中国已成为点支承玻璃幕墙的使用大国和技术强国,各种形式的点支承玻璃幕墙在中国得到了应用和发展。由于支承结构具有通用性,所以在点支承玻璃幕墙中,最能代表其技术发展的就是玻璃面板的点连接方式。布近半个世纪的发展过程中,玻璃面板的连接方式先后有过补丁板式连接系统(图1)、皮尔金顿平面系统(图2)、铰接螺栓系统“(图3)。存这些基本系统的基础上,目前已形成现在主流的几种点支承方式:玻璃开孔点支承(图4)、玻璃边点支承(图5)和玻I离角点支承(图6),其中玻璃角点支承方式由于承重高、造价低等优点,近年来在行业中的发展最为迅速。玻璃角点支承中的支承装置行业内通常称之为夹具(见图6),它是点支承玻璃幕墙工程中集合了驳接头和驳接爪功能与一体的一种复合连接件,其前面槽口用于安装固定玻璃,槽口内部的玻璃与金属部件之间衬有柔性垫片,后面部分相连支承结构。

由于夹具支承玻璃的面积相对于整块玻璃而言要小得多,所以行业内也将这种方式视为一种点支承方式。点支承方式是一种局部支承方式,所以应力集中问题始终存在,唯—的办法是尽量减小应力集中的程度。对于四点支承的玻I离面板而言,行业内传统的观念认为玻璃面板在面外荷载的作用下,其最大应力不出现在支承点附近,而出现在长边跨中即认为玻I离面板的应力分布是比较合理的。理论与实践订明,这主要取决于支承点对玻璃的转动约束程度,约束越弱面板应力分布越接近于这种理想状态;所以点支承玻璃幕墙中常用的驳接头都设计有球铰。对于玻璃夹具而言,由于构造不同j不能在上面装上像驳接头一样的球铰,要实现这种功能只能采取其它的技术措施。目前行业内有两种做法:主流的做法是在夹具与玻璃之间垫上适当厚度的橡胶垫片,利用橡胶的超弹性来实现对玻璃固定点的铰接支承(图7)i另一种做法是在夹具内玻璃角部两侧安装上半球形垫块,利用这种物理意义的球铰装置来实现对玻璃固定点的铰接支承(图8)。从一般的力学常识来判断的话,这两种做法都是有道理的,但是在实际的工程应用中,这两种支承方式能否达到预想的效果?各有什么优缺点?目前在行业中这方面的研究比较少,国外也很少见到关于这方面的技术文献。
本文利用有限元分析软件的三维实体分析功能,对圉前点支承玻璃幕墙中常见的这两种铰接支承方案做了分析对比,以供设计者参考。目前能够精确分析这类问题的都是一些大型的有限元分析软件, 如美国HKS公司ABAQUS软件, ANSYS公司开发的ANSYS软件。本文的对比分析采用ANSYS软件来进行。

2.分析模型及分析说明
2.1分析对象
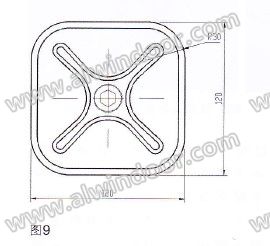
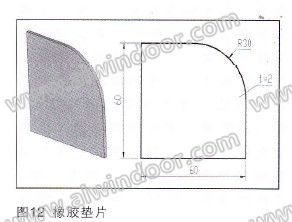
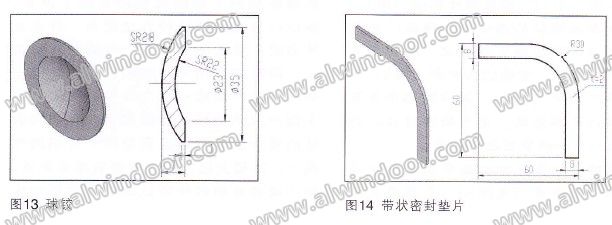
本文所取的玻璃为12mm厚钢化玻璃面板分格尺寸为1800mm×2000mm,采用四点支承方式,所选夹具规格为120mm×120mm(图9)。承受外面均布荷载q=2kN/m2,自重作用忽略。支承方式分别为实际点支承(支承在有限元节点上)、橡胶垫片支承(图10)`球铰支承(图11)。

2.2材料特性
2.2.1玻璃
玻璃是一种典型的脆性材料;导致其发生脆性断裂破坏的原因是其最大拉应力达到了材料的抗拉强度。因此在校核时适用最大拉应力理论(或称第一强度理论),本文所显示的玻璃应力均为第一主应力S1。玻璃在分析时,其弹性模量E=0.72× 105N/mm2, 泊松比v=0.2。
2.2.2球铰材质
球铰可选用多种材质制造,本文选用建筑行业中常用的尼龙66(PA66)。尼龙66自勺复合产品较多,参数不一,本文假设其弹4哇模量为3000N/mm2, 泊松比v=0,强度校核采用最大切应力理论(或称第三强度理论)。本文所显示的球铰应力均为VOnMises等效应力。
 上一页123下一页
上一页123下一页
